私たちの周りはさまざまな物質であふれている。これら物質を原子や分子のレベルで考える学問、それが "chemistry" だ。物質の世界に魅了され、原子・分子レベルで、物性、及びそれらの反応性について追究していく者が化学者である。化学者はさまざまな方法で物質に対しアプローチをかける。「実験」を通して試みる者もいれば、「観測」を通じて触れ合う者もいる。そのような中で私たちは計算機を道具として使い、「理論」から物質を見つめることでアプローチしている。

　化学の問題は少なくとも原理的には量子力学で全て解決できると言われている^*1。しかし、普通、私たちが取り扱う化学的な事象は、大抵、原子や分子が複雑に関わっており、それらを量子力学的にまともに扱うことは事実上不可能である。それは、分子系の電子状態を完全に知るためには、多電子系のシュレディンガー波動方程式を解く必要があるためである。水素原子やヘリウムイオンなどの一電子一中心系のものを除いて数学的にこの方程式を厳密に解くことは出来ない。したがって、量子力学を化学に適用するにあたっては、いかに優れた近似理論を確立するかということが非常に重要なのである。

　当研究室では、1999年に京都大学(当時は大阪府立大学に所属)の北浦先生により提唱された
　　フラグメント分子軌道法（ Fragment Molecular Orbital method；FMO法 ）^*2
を推進している。 FMO法は、分子系をフラグメントに分割(たとえばタンパク質ならアミノ酸残基ごとに分割)し、フラグメントのモノマーとダイマーから分子全体を構成させて計算する方法である。それらは、周囲のモノマーからの環境静電ポテンシャル(静電ポテンシャル)のもとで計算され、分子系全体のエネルギーや電子密度を知ることが出来る。FMO法の利点として、フラグメントごとに分けて分子軌道計算を行うことで、分子全体を一度に取り扱う必要が無く、フラグメント単位で並列処理をすることが可能となることが挙げられる。これにより、計算量（計算時間）の増加を解決することが出来る。したがって、第一原理に基づいて大きな分子の電子状態計算を行うことが出来るため、分極や電荷移動を伴う分子認識、巨大なタンパク質から構成される酵素の反応、さらには光合成反応のようなタンパク質の励起状態にも適用できる方法である。また、フラグメントに分けて計算を行うということは、単にコストを抑えて分子全体について知ることが出来るというだけではない。分子の局所的な性質について知ることが出来るという点もFMO法を使う重要な意義である。 FMO 法の計算の流れは以下の通りである。

　　　　　　　　　

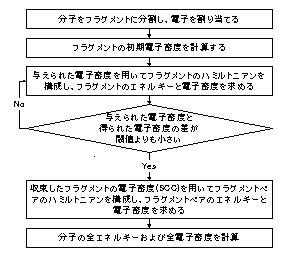
　FMO法の特徴のひとつに、フラグメント間相互作用エネルギー( Inter-Fragment Interaction Energy；IFIE )の計算がある。IFIEを用いると、たとえば特定のアミノ酸残基とリガンド化合物の相互作用を詳細に解析することが可能であり、FMO法は創薬などの分子設計の現場で使える実用的な解析ツールとなっている。^*3
　
FMO法の実装は、産総研の Fedorov 博士らによる GAMESS 版、豊橋技術科学大学の関野博士らによる NWChem への組み込み、文部科学省次世代 IT 基盤構築のための研究開発プログラム「革新的シミュレーションソフトウェアの研究開発（ RSS21 ）」プロジェクト、及び JST CREST 「フラグメント分子軌道法による生体分子計算システムの開発」プロジェクトを中心に開発が進められている ABINIT-MP などがある。当研究室は ABINIT-MP を基本プラットフォームとしてエンジン開発を進め、応用計算を行っている。

　ABINIT-MP の基礎となる ABINIT は筑波大学 化学系 物理化学研究室（菊池研・当時）で開発された。 ABINIT-MP は国立医薬品食品衛生研究所の中野博士が、タンパク質と薬品分子の相互作用の電子状態レベルでの解析を目的とし、FMOスキームに基づきその原版を開発したものである。現在、 ABINIT-MP は FMO-HF^*4からその機能は拡張され続けている。

・Post-HFとして
　階層化CIS/CIS(D)の開発
　高速な MP2 計算エンジンの開発^*5,6
（生体系分子を扱う場合、水素結合の他に分散力に基づいた van der Waals 相互作用や疎水性相互作用が重要である。しかしながら、HF法では分散力を記述することは出来ない。 MP2法は水素結合や分散力を扱うことの出来る安全な手法である。）
・積分計算の改良・基底関数の向上
・フラグメント間の相互作用エネルギーの解析ツールの開発
　　― IFIE ( Inter-Fragment Interaction Energy )
・フラグメント間の配置解析ツールの開発^*7,8
　　― CAFI ( Configuration Analysis for Fragment Interaction )
　　― CERF ( Concurrent Electron Relaxation Functional )
・物性値解析^*9
　　― CPHF/LR (Coupled Perturbed Hartree-Fock / Linear Response )
　etc...


　私たちの FMO 計算に関するスタンスは次の通りである。

　まず、自主プログラムを開発するという点。先に挙げた GAMESS などへの実装は既存の機能を使って FMO 化されている。しかし、私たちは国産のプログラムを死守することを目的とし、ゼロからプログラムの開発を行う。これにより、前者と比べると作業は遅くなるが、"空洞化はしない"ということで確実に前に進んでいくことができる。また、日本では"応用計算化学"という面が米欧に比すと極めて強く、本格的にコード開発が出来るグループは少ない。ソフトウェアの"大幅な輸入超過"によって量子化学・計算化学が支えられているという状況であり、長期的に見ればかなり危険であると思われる^*10。この様な点も踏まえ、日本のプログラムを厳守するという信念のもと、外部の研究グループと交流をはかりながら日々研究に取り組んでいる。
　次に、応用計算も推進するという点。実験・医薬・情報科学・計算機分野などの専門家とコラボレーションをすることにより、光応答タンパク質やDNA、薬物系、シリコン材料などに対する応用計算や、応用計算を視野に入れた理論・プログラム開発を行っている。




Reference

　[1] 米澤貞次郎, 永田親義, 加藤博史, 今村詮, 諸熊奎冶 量子化学入門（上） 化学同人 1,4 (1983)
　[2] K. Kitaura, E. Ikeo, T. Asada, T. Nakano, M. Uebayasi, Chem. Phys. Lett. 313, 701-706 (1999).
　[3] 佐藤文俊, 中野達也, 望月祐志 プログラムで実践する生体分子量子化学計算　森北出版（2008）
　[4] T. Nakano, T. Kaminuma, T. Sato, K. Fukuzawa, Y. Akiyama, M. Uebayasi, K. Kitaura, Chem. Phys. Lett. 351, 475-480 (2002).
　[5] Y. Mochizuki, T. Nakano, S. Koikegami, S. Tanimori, Y. Abe, U. Nagashima, K. Kitaura, Theor. Chem. Acc. 112, 442-452 (2004).
　[6] Y. Mochizuki, S. Koikegami, T. Nakano, S. Amari, K. Kitaura, Chem. Phys. Lett. 396, 473-479 (2004).
　[7] Y. Mochizuki, K. Fukuzawa, A. Kato, S. Tanaka, K. Kitaura, T. Nakano, Chem. Phys. Lett. 410, 247-253 (2005).
　[8] Y. Mochizuki, Chem. Phys. Lett. 410, 165-171 (2005).
　[9] Y. Mochizuki, T. Ishikawa, K. Tanaka, H. Tokiwa, T. Nakano, and S. Tanaka, Chem. Phys. Lett. 418, 418-422 (2006).
　[10] 望月祐志 "米欧日の量子化学ソフトウェアの現状と今後の展望" 21世紀の産業革命 コンピュータ・シミュレーション 戦略的基盤ソフトウェア産業応用推進協議会編 アドバンスソフト (2004)