![]()
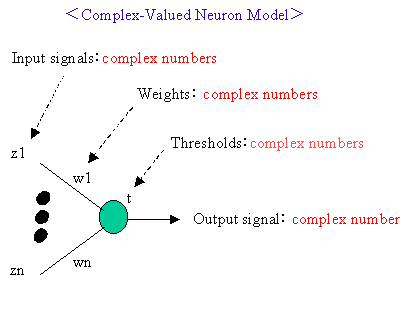
The complex-valued Neural Network is an extension of a (usual) real-valued neural network, whose input and
output signals and parameters such as weights and thresholds are all complex
numbers (the activation function is inevitably a complex-valued function).
Neural Networks have been applied to various fields such as communication systems, image
processing and speech recognition, in which complex numbers are often used through the Fourier Transformation. This indicates that complex-valued neural networks are useful. In addition, in the human brain, an action potential may have
different pulse patterns, and the distance between pulses may be different.
This suggests that introducing complex numbers representing phase and amplitude into neural networks is appropriate.
In these years the complex-valued neural networks expand the application
fields in image processing, computer vision, optoelectronic imaging, and
communication and so on. The potentially wide applicability yields new
aspects of theories required for novel or more effective functions and
mechanisms.
| Merits of complex-valued neural networks | (1) Representation of information Since the input and output signals are supposed to be complex numbers (i.e., 2 dimensions), the complex-valued neural networks can represent 2-dimensional information naturally, needless to say complex-valued signals. (2) Characteristics of learning The learning speed of the complex-valued back-propagation learning algorithm (called Complex-BP) for multi-layered complex-valued neural networks is 2 or 3 times faster than that of the real-valued one (called Real-BP). In addition, the required number of parameters such as the weights and the thresholds is only about the half of the real-valued case. An example of the application: (a) The authors applied the Complex-BP algorithm to the recognition and classification of epileptiform patterns in EEG, in particular, dealing with spike and eye-blink patterns. They reconfirmed the characteristics of learning described above. Reference:De Azevedo, F. M., Travessa, S. S. and Argoud F. I. M.., "The Investigation of Complex Neural Network on Epileptiform Pattern Classification", Proc. The 3rd European Medical and Biological Engineering Conference (EMBEC'05) , pp.2800-2804, 2005. An example of the improvement of the Complex-BP algorithm: (a) The authors proposed a modified error function by adding a term to the conventional error function in order to speed up the learning process. Reference: Chen, X., Tang, Z, Variappan, C., Li, S. and Okada, T., "A Modified Error Backpropagation Algorithm for Complex-valued Neural Networks", International Journal of Neural Systems, Vol.15, No.6, pp.435-443, 2005. |
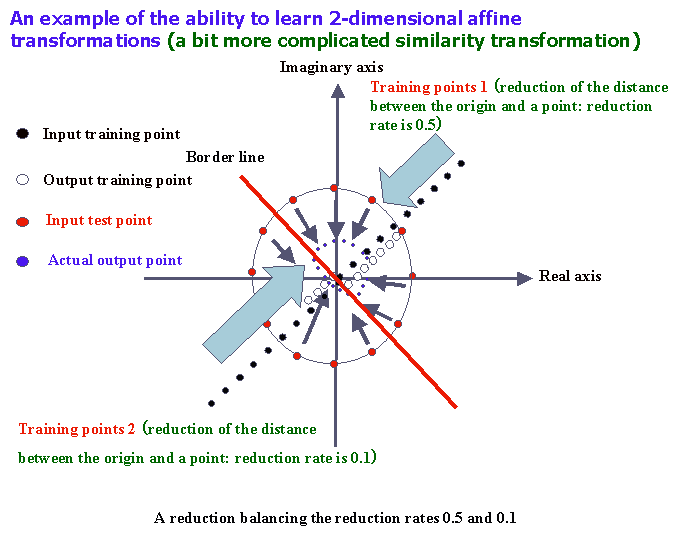
| Inherent properties of complex-valued neural networks | (1) Ability to learn 2-dimensional affine transformations The complex-valued neural network can transform geometric figures, e.g. rotation, similarity transformation and parallel displacement of straight lines, circles, etc.. Examples of the application of the abiilty to learn 2-dimensional affine trnasformations: (a) Application to the estimation of optical flows in the computer vision Reference: Watanabe, A. et al., "A Method to Interpret 3D Motion Using Neural Networks", IEICE Trans. Fundamentals, Vol.E77-A, No.8, pp.1363-1370, 1994. (b) Application to the generation of fractal images Reference: Miura, M. and Aiyoshi, E.., "Approximation and Designing of Fractal Images by Complex Neural Networks", IEEJ Trans. EIS,Vol.123,No.8,pp.1465-1472, 2003 (in Japanese). (2)Orthogonality of decision boundaries A decision boundary of a complex-valued neural network basically consists of two hypersurfaces that intersect orthogonally, and divides a decision region into four equal sections. Several problems that cannot be solved with a single real-valued neuron, can be solved with a single complex-valued neuron using the orthogonal property. (3)Structure of critical points The critical points (satisfying a certain condition) of the complex-valued neural network with one output neuron caused by the hierarchical structure are all saddle points, not local minina, unlike the real-valued case where a critical point is a point at which the derivative of the loss function is equal to zero. |