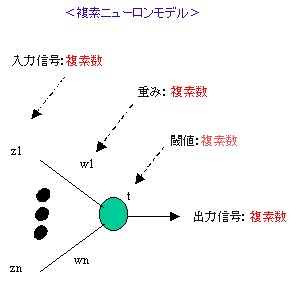
複素ニューラルネットワークとは,入出力信号やパラメータ(重み,閾値)が複素数値であるようなニューラルネットワークです(活性化関数は必然的に複素関数になります)。
世の中の多くのシステムは複素数(波動:位相と振幅)で表現されることがよくあります。たとえば,通信,音声処理,画像処理などの分野ではフーリエ変換を通じて複素数が現れます。近年,これらの分野を中心に複素ニューラルネットワークの応用が広がりつつあります。
複素ニューラルネットワーク
複素ニューラルネットワークとは,入出力信号やパラメータ(重み,閾値)が複素数値であるようなニューラルネットワークです(活性化関数は必然的に複素関数になります)。

世の中の多くのシステムは複素数(波動:位相と振幅)で表現されることがよくあります。たとえば,通信,音声処理,画像処理などの分野ではフーリエ変換を通じて複素数が現れます。近年,これらの分野を中心に複素ニューラルネットワークの応用が広がりつつあります。
| 複素ニューラルネットワーク の利点 |
(1) 情報の表現 入力信号と出力信号が複素数(2次元)であるため,複素数で表現された信号はもとより,2次元情報を自然に表現することができます。 (2) 学習特性 階層型の複素ニューラルネットワークの学習速度は,実ニューラルネットワークに比べて 2〜3倍速く,しかも必要とするパラメータ(重みと閾値)の総数が約半分で済みます(複素逆誤差伝播学習アルゴリズム(複素BP)を使用した場合)。 応用例: 複素BPが,EEG(脳波データ)における”てんかん”の症状によって引き起こされるパターンと”目のまばたき”によって引き起こされるパターンとを識別することに応用されました。その過程で,複素BPに関する上記で述べた学習特性が再確認されました。 参考文献:De Azevedo, F. M., Travessa, S. S. and Argoud F. I. M.., "The Investigation of Complex Neural Network on Epileptiform Pattern Classification", Proc. The 3rd European Medical and Biological Engineering Conference (EMBEC'05) , pp.2800-2804, 2005. 改良例: 複素BP学習アルゴリズムが高速化されました。活性化関数にある項を追加することによって,ローカルミニマムを避けるように改良されました。 参考文献:Chen, X., Tang, Z, Variappan, C., Li, S. and Okada, T., "A Modified Error Backpropagation Algorithm for Complex-valued Neural Networks", International Journal of Neural Systems, Vol.15, No.6, pp.435-443, 2005. |
| 複素ニューラルネットワーク 固有の特性 |
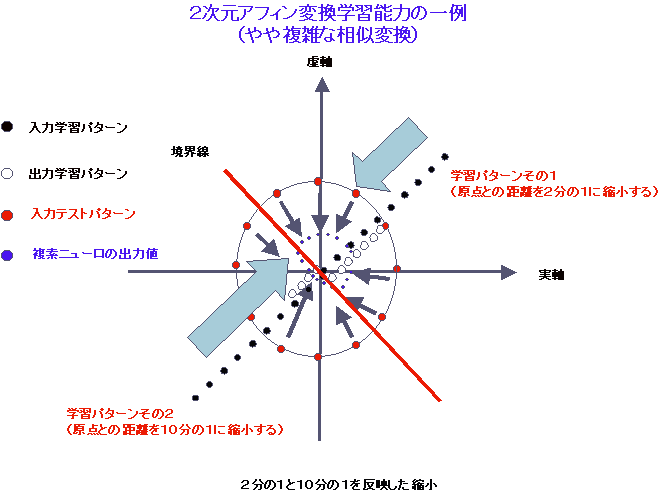
(1) 2次元アフィン変換学習能力 平面図形の変換能力があります。たとえば,平面図形の「一部分」を縮小させるような学習パターンを複素ニューラルネットワークに学習させると,平面図形の「他のすべての点達」もその縮小率に従って縮小されます。拡大,回転,平行移動あるいはそれらを組み合わせた変換についても同様です。 応用例: (a) コンピュータビジョンにおけるオプティカルフローの推定に,2次元アフィン変換学習能力が応用されました。 参考文献:Watanabe, A. et at., "A Method to Interpret 3D Motion Using Neural Networks", IEICE Trans. Fundamentals, Vol.E77-A, No.8, pp.1363-1370, 1994. (b) フラクタル図形の生成に2次元アフィン変換学習能力が応用されました。 参考文献: 三浦 みちる,相吉 英太郎,"複素ニューラルネットワークによるフラクタル図形の近似と設計", 電気学会論文誌,123巻,8号,pp.1465-1472, 2003年. (2)決定表面の直交性 パターン識別を行う際に形成される決定表面が基本的に互いに直交する2つの超曲面から構成されます。この特性をうまく使うことにより,従来,単一の実ニューロンで解けなかった問題が単一複素ニューロンで解けます。 (3)危点の構造 1出力の複素ニューラルネットワークの(階層構造に起因する)ある条件を満たす危点(損失関数を微分して0になる点)は,実ニューラルネットワークと違って,必ず鞍点になります(ローカルミニマム(局所解)にはなりません)。 |